Como programar um computador quântico
Como fazer Battleships de quantum NOT gates

Os computadores quânticos são um novo tipo estranho de computador. Eles criam números impensáveis de universos paralelos para executar programas mais rapidamente e usam princípios que confundem até mesmo Einstein. Eles são as mágicas caixas de milagres que vão deixar suas estúpidas caixas de transistores na poeira.
Isso é o que os artigos científicos populares provavelmente dirão a você, de qualquer maneira. Eles sem dúvida conseguem fazer com que essa nova tecnologia pareça excitante. Mas eles também podem fazer a computação quântica parecer uma arte arcana, confiada apenas aos cientistas mais inteligentes. Certamente não é algo para o público de programação mais amplo para se preocupar com!
Eu não acho que isso seja verdade. E com empresas como a IBM e o Google, na verdade, fabricando dispositivos quânticos, a hora de começar a brincar com a programação quântica é agora.
Você não precisa fazer nada extravagante no começo. Você pode começar sua jornada na programação quântica no mesmo lugar em que muitos de nós começam nossa jornada na programação normal: fazendo jogos.
Não se preocupe, não será necessário ter seu próprio computador quântico. Programas quânticos simples podem ser facilmente simulados em um computador normal. Também podemos emprestar algum tempo em um dispositivo quântico real, graças ao IBM Q Experience .
Este é o primeiro de uma série de artigos nos quais descrevo alguns programas simples feitos usando o quantum SDK da IBM. Cada um será uma versão independente dos Battleships, com processos quânticos simples usados para implementar a mecânica básica do jogo.
Estes estão entre os primeiros jogos feitos para um computador quântico. Mostrarei os detalhes sangrentos do código por trás do jogo, para que você possa começar a experimentar também a programação quântica.
O que é um computador quântico?
Antes de começarmos o programa, precisamos de algumas informações básicas. Não vou contar tudo sobre computação quântica. Nós vamos conseguir o suficiente para entender o que acontece no nosso jogo.
Um computador normal é baseado em bits: variáveis que possuem apenas dois valores possíveis. Muitas vezes os chamamos 0 e 1, embora no contexto da álgebra booleana, podemos chamá-los Truee False. Não importa o que nós chamamos. O ponto importante é que existem apenas dois estados.
Com bits podemos fazer operações booleanas simples, como NOT, AND e OR. Estes são os blocos de construção básicos da computação. Com estes podemos fazer qualquer coisa. Qualquer variável mais complexa que um bit (como um int ou float) é apenas uma coleção de muitos bits. Qualquer operação mais complexa que um AND ou NOT é, na verdade, apenas muitas delas juntas. Em seu nível mais básico, isso é o que um computador normal é.
Os computadores quânticos são baseados em bits quânticos ou qubits. Estes também têm dois valores possíveis que podemos chamar 0e 1. Mas as leis da mecânica quântica também permitem outras possibilidades, que chamamos de estados de superposição.
Em certo sentido, os estados de superposição são valores que existem a meio caminho entre os extremos de 0 e 1. Podemos imaginar um qubit como uma esfera, com 0 e 1sentando em postes opostos. Os estados de superposição são todos os outros pontos possíveis na superfície.
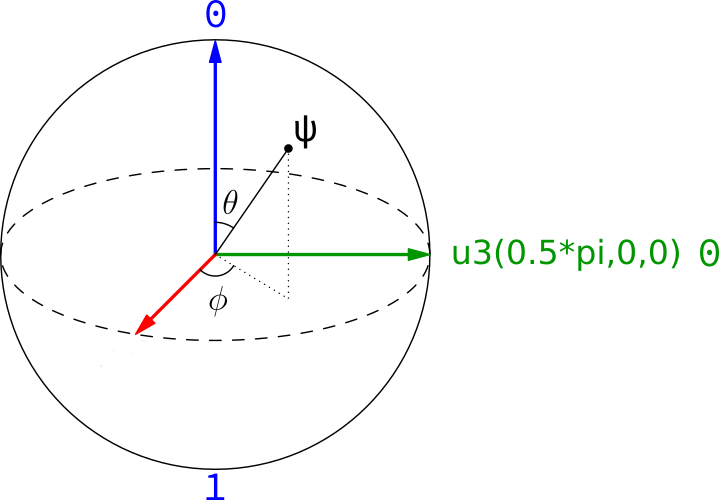
Além de 0 e 1, essa imagem também sinaliza alguns estados de superposição importantes. Um é chamado u3(0.5*pi,0,0) |0⟩. É certo que não é um nome muito cativante, mas vamos ver o que realmente significa durante este artigo.
Esse modo de pensar sobre qubits faz com que pareçam um pouco com variáveis contínuas. Podemos representar qualquer ponto na superfície de uma esfera (como o ponto ψ na imagem) usando coordenadas polares com apenas alguns ângulos (θ e φ). Então você seria perdoado por pensar que um qubit é apenas um par de carros alegóricos. De certa forma, eles são. Mas em outro sentido mais preciso, eles não são.
Uma diferença importante é que nunca podemos extrair mais do que uma informação binária de um qubit. As próprias leis da física nos impedem de descobrir exatamente o que estão fazendo. Não podemos pedir um qubit para os detalhes exatos do estado de superposição. Nós só podemos forçá-lo a escolher entre dois pontos opostos na esfera (como 0 e 1). Se for algo diferente desses dois estados, terá que decidir aleatoriamente um ou outro.
Portanto, um qubit tem algumas propriedades de uma variável contínua e algumas propriedades de uma variável discreta. Na verdade, não é nenhum dos dois. É uma variável quântica.
O que faremos com os qubits?
O jogo Battleships que estamos fazendo hoje é baseado em uma variante japonesa. Nisso, todos os navios ocupam apenas um único quadrado, mas alguns demoram mais para afundar do que outros. Teremos um navio que pode ser afundado por uma única bomba, um que precisa de dois e um que precise de três.
Para simular isso em um computador quântico, podemos usar um qubit para cada nave. O estado 0 pode ser identificado com um navio totalmente intacto e 1 com um que tenha sido destruído. Os estados de superposição corresponderão então à jornada de um navio rumo à destruição.
Um navio destruído por um único ataque será muito fácil de simular. Podemos inicializá-lo no estado 0 e, em seguida, aplicar um NOT quando for atingido. Quando o encontrarmos em estado 1, saberemos que foi destruído.
Vamos ver como implementar apenas esse processo simples em um computador quântico. Não nos preocuparemos com quaisquer outros navios, ou entradas e saídas no momento.
Para fazer isso, usaremos o SDK quântico QISKit para configurar um programa quântico. Aqui está um script que inicializa uma nave, a bombardeia e depois analisa se ela ainda está flutuando.
q = QuantumRegister(1) # inicializa um registrador com um único qubit
c = ClassicalRegister(1) # inicializa um registrador com um bit normal
qc = QuantumCircuit(q, c) # cria e esvazia o programa quântico
qc.u3(math.pi,0,0, q[0]) # aplica um NOT ao qubit
qc.measure( q[0], c[0] ) # mede o qubit
Primeiro, isso define todos os bits que precisaremos: tanto quantum quanto normal. Neste exemplo nós definimos um único qubit em um registrador chamado q. Nós nos referimos a este qubit no código como q[0]. Como as saídas precisam estar em uma informação normal agradável, legível por humanos, também definimos um único bit normal em um registro chamado c.
O qubit q[0] é automaticamente inicializado no estado 0. Como esse é o estado que queremos começar, nenhuma preparação adicional é necessária.
Em seguida, queremos levar isso q[0] = 0, uma nave totalmente intacta e executar um NOT. Com um bit normal e uma linguagem normal de programação, podemos implementar isso como q[0] = !q[0] (para C ++) ou q[0] = not q[0] (para Python). No QISKit isso pode ser feito de várias maneiras. O mais simples é usar operações chamadas x e y. Aqui estão alguns exemplos de como usá-los, com as linhas equivalentes de C++ e Python para comparação.
q[0] = !q[0]; \\ A C++ style NOT
q[0] = not q[0] # A Python style NOT
qc.x( q[0] ) # A QISKit style NOT
qc.y( q[0] ) # Another QISKit style NOT
Existem algumas diferenças entre x e y que vamos ter de lidar com isso um dia. Mas não hoje.
Você provavelmente já notou que x nem y aparece no trecho anterior do QISKit. Em vez disso, temos u3(pi, 0,0). Esta é outra maneira de implementar um NOT.
qc.u3(math.pi,0,0, q[0]) # Yet another QISKit style NOT
Esta operação é completamente equivalente a y. Mas u3 é uma operação mais complexa em geral. Tem três argumentos e, alterando-os, podemos fazer outras coisas.
Note que ao implementar esta operação no QISKit, ele recebe um quarto argumento, que é o qubit ao qual estamos aplicando.
O primeiro argumento é um ângulo expresso em radianos. É o ângulo pelo qual vamos girar a esfera do nosso qubit. O ângulo pi (ou math.pi quando implementado em Python) corresponde a 180 °. Isso significa que nós viramos a esfera completamente de cabeça para baixo. 0 move-se para 1 e 1 move-se para 0, razão pela qual esta operação atua como NOT. Para fazer meia NOT poderíamos simplesmente usar metade desse ângulo: u3(0.5*pi,0,0).
Então, agora nós temos ainda uma outra maneira de executar um NOT em nosso qubit: Nós poderíamos fazer meio NOT duas vezes.
# Another QISKit style NOT
qc.u3(math.pi/2,0,0, q[0])
qc.u3(math.pi/2,0,0, q[0])
Nós também podemos fazer um terço de um NOT três vezes, ou um quarto de um NOT seguindo por meio NOT e, em seguida, dois oitavos de um NOT. Você entendeu a ideia.
A última linha do nosso trecho QISKit é
qc.measure( q[0], c[0] )
Neste nós medimos o qubit. Nós dizemos q[0] que tem que decidir o que ser: 0 ou 1. O resultado é então armazenado c[0], pronto para ser examinado por nossos cérebros não-quânticos, ou processado por nossos computadores não-quânticos. O valor de c[0] é então a saída desse cálculo.
Se não fizemos nada entre inicialização e medição …
q = QuantumRegister(1)
c = ClassicalRegister(1)
qc = QuantumCircuit(q, c)
qc.measure( q[0], c[0] )
… O resultado deve ser sempre c[0] = 0.
Se nós fizemos um NOT …
q = QuantumRegister(1)
c = ClassicalRegister(1)
qc = QuantumCircuit(q, c)
qc.u3(math.pi,0,0, q[0])
qc.measure( q[0], c[0] )
..o resultado deve ser sempre c[0]=1.
Se fizéssemos apenas meio NOT …
q = QuantumRegister(1)
c = ClassicalRegister(1)
qc = QuantumCircuit(q, c)
qc.u3(0.5*math.pi,0,0, q[0])
qc.measure( q[0], c[0] )
… q[0] Estará na metade do caminho entre 0 e 1 quando for medido. Na verdade, será o estado de superposição que chamamos u3(0.5*pi,0,0) |0⟩ anteriormente. Medindo se isso é 0 ou 1 vai forçá-lo a escolher aleatoriamente um ou outro, com probabilidades iguais.
Essa natureza probabilística vai aparecer em cálculos quânticos. A aleatoriedade adicional também está presente nos dispositivos atuais devido ao ruído. Embora isso esteja em um nível geralmente baixo, ainda temos que manter sua existência em mente. Então, às vezes, teremos um 1 quando devemos receber um 0 e vice-versa.
Por essas razões, é comum executar um programa quântico muitas vezes. Em seguida, esse processo retorna uma lista de todas as saídas geradas durante essas várias amostras e o número de vezes que ocorreram.
Fazendo um jogo
Agora vamos usar esses muitos caminhos em direção a NOT para fazer um jogo em um computador quântico.
Primeiro, vou deixar você em segredo. Computadores quânticos sempre serão dispositivos híbridos, parcialmente quânticos e parcialmente normais. O último é necessário para lidar com entradas e saídas, a fim de interagir com os macacos que querem usar o dispositivo.
Por esse motivo, os SDKs quânticos geralmente são incorporados em uma linguagem de programação padrão. O QISKit usa o Python, portanto, podemos usar um programa Python para lidar com as partes normais do programa e para construir e executar tarefas para a parte quântica.
É importante notar que tudo ainda está evoluindo. E todos nós fazendo programas quânticos nestes primeiros dias, inevitavelmente, guiaremos essa evolução.
Para executar o programa, você precisará do Jupyter instalado, bem como das dependências do SDK. Você pode encontrar mais aqui.
Agora vamos ver o código!
Em primeiro lugar, tudo o que precisamos para executar o código no Quantum Experience da IBM precisa ser importado.
from qiskit import ClassicalRegister, QuantumRegister
from qiskit import QuantumCircuit, execute
Em seguida, precisamos nos registrar com a API para que possamos realmente executar tarefas no dispositivo quântico real.
from qiskit import register
import Qconfig
qx_config = {
"APItoken": Qconfig.APItoken,
"url": Qconfig.config['url']}
register(qx_config['APItoken'], qx_config['url'])
Isso faz referência ao Qconfigarquivo, no qual você precisará de uma conta com a IBM para configurar. Não se preocupe, é grátis! Veja aqui os detalhes.
Em seguida, importamos várias funções projetadas para lidar com todas as entradas e saídas chatas. Como isso não faz parte da programação quântica, não entraremos em detalhes sobre isso.
from battleships_engine import *
A primeira coisa que precisamos fazer é decidir sobre o dispositivo que será usado para a parte quântica do programa.
device = ask_for_device()
from qiskit import Aer, IBMQ
try:
backend = Aer.get_backend(device)
except:
backend = IBMQ.get_backend(device)
A função ask_for_device() simplesmente pergunta ao jogador se deve ou não usar o dispositivo real. Se eles responderem y, o dispositivo escolhido é ibmq_5_tenerife: um processador quântico real de cinco qubits nos laboratórios da IBM. Se eles responderem n, um simulador é escolhido.
Outra coisa importante a definir é o número de vezes que cada trabalho será executado. Isso ocorre porque usamos muitas amostras para calcular estatísticas sobre as saídas possivelmente aleatórias que recebemos.
shots = 1024
Não há razão mágica para 1024. Você pode mudá-lo se quiser.
Em seguida, chegamos a montar as pranchas, com cada jogador escolhendo onde colocar três navios. Cinco posições possíveis estão disponíveis, correspondendo aos cinco qubits do dispositivo ibmqx4 da IBM. Eu visualizo a grade assim
4 0
|\ /|
| \ / |
| \ / |
| 2 |
| / \ |
| / \ |
|/ \|
3 1
Os números são os nomes que eu uso para cada posição. Eles também são os nomes que a IBM usa, assim 2 como a posição do qubit q[2], por exemplo.
As escolhas feitas pelos jogadores são armazenadas em shipPos. Isto tem uma entrada para cada um dos dois jogadores ( player=0 para o primeiro jogador, player=1 para o segundo) e para cada um dos três navios que eles colocam. A entrada shipPos[player][ship] mantém a posição ( 0, 1, 2, 3ou 4) para o navio numerados shippertencente a player.
Agora é hora do loop principal do jogo. Neste vamos perguntar a ambos os jogadores onde na grade do seu oponente eles gostariam de bombardear. Isto é então adicionado bomb[player][position], o que conta quantas vezes player bombardeou position ao longo do jogo.
Agora temos informações suficientes para configurar o programa quântico. Sabemos quais qubits devem ser navios e onde bombardear. Então agora é hora de definir os trabalhos correspondentes com o QISKit.
Em cada rodada teremos dois programas quânticos para executar: cada um simulando a ação na grade de um jogador. Vamos usar o array qc para manter esses programas.
qc = []
for player in range(2):
q = QuantumRegister(5)
c = ClassicalRegister(5)
qc.append( QuantumCircuit(q, c) )
Cada programa é inicializado com um registro de cinco bits quânticos e clássicos, para cobrir toda a grade. O programa para a grade de um determinado jogador pode ser endereçado qc[player], embora note que o jogador 1 é aqui referido como player=0, e o jogador 2 como player=1.
Agora, suponha que queremos aplicar uma certa fração de um NOT a um determinado qubit. Nós fazemos isso com a seguinte linha
qc[player].u3(frac * math.pi, 0.0, 0.0, q[position])
mas com frac e position substituídos por números reais.
Usando isso, podemos adicionar todas as bombas que o jogador adversário está disparando nessa grade. Para a grade de player nós circulamos sobre as três posições onde há um navio. Em seguida, adicionamos uma linha qc[player] para cada bomba que foi enviada aqui.
Mencionei anteriormente que os três navios neste jogo terão diferentes pontos fortes. O primeiro colocado pelo jogador será afundado por uma única bomba, mas o segundo precisará de dois para ser destruído e o terceiro precisará de três.
Em termos de qubits, isso significa que uma bomba que atinge o primeiro navio aplica um NOT inteiro. Uma bomba que atinge o segundo navio se aplica, metade de um NOT, e um no terceiro navio aplica um terço de um NOT. A fração frac é então determinada por qual navio está sendo atingido. Para isso, simplesmente usamos frac = 1/(ship+1).
Uma vez que o bombardeio acabou, é hora de ver o que aconteceu. Para isso, precisamos adicionar os comandos de medição. Cada qubit no registrador é medido e os resultados copiados para um bit normal correspondente. Isso é feito com
for qubit in range(5):
qc[player]t.measure(q[qubit], c[qubit])
Agora temos um par de programas quânticos, é hora de executá-los. Isso é feito usando
job = execute(qc, backend, shots=shots)
Aqui backend foi definido anteriormente quando perguntamos ao jogador em qual dispositivo rodar.
Depois que o trabalho for enviado, podemos tentar extrair os dados.
for player in range(2):
grid[player] = job.result().get_counts(qc[player])
Aqui eu copio os resultados para grid, com os resultados do bombardeio dos playernavios em grid[player].
Observe que a chamada job.result() irá aguardar até que o trabalho tenha realmente parado de ser executado. Se você estiver em uma fila atrás dos outros usando o dispositivo, isso pode levar alguns minutos.
Os resultados são armazenados grid[player] como um dicionário. As chaves são seqüências de bits e assim parecem algo 110. O bit mais à direita é c[0], e assim c[0]=0, neste exemplo de seqüência de bits. Ao processar os resultados, podemos descobrir quantas execuções receberam cada resultado ( 0 ou 1) para cada um dos bits normais.
Nós interpretamos a fração de vezes que um qubit é medido para ser 1 como o dano percentual para o nosso navio. Nós não podemos esperar 100% de dano devido aos efeitos do ruído (ou tempo, se você quiser uma explicação no universo) então nós contamos um dano maior que 95% como significando que a nave afundou.
Vamos verificar alguns exemplos de saídas do processo quântico. Suponha que um jogador coloque seu terceiro navio na posição 2. O outro jogador então o bombardeia. Os resultados serão parecidos.
{'00000': 734, '00100': 290}
Aqui, 290 das 1024 corridas encontraram uma 1 posição 2, mostrando que esta nave realmente sofreu alguns danos.
Outro exemplo: um jogador coloca seu primeiro navio na posição 1 e o segundo em 2. O outro jogador lança a primeira posição na primeira rodada e a segunda posição na segunda. Os resultados seriam
{'00110': 532, '00010': 492}
Aqui todos os resultados têm um 1segundo slot à direita (o da posição 1). Aquela nave foi destruída por uma única bomba. O que está na posição 2 foi apenas meio danificado, portanto, metade dos resultados tem um 1para isso.
Estes resultados de exemplo foram bons e limpos, então podemos dizer que eles foram feitos no simulador. No dispositivo real, você pode encontrar alguns 1 para resultados de navios que não foram bombardeados e para qubits que não são navios.
O processamento de cadeias de bits não é algo exclusivo da computação quântica, por isso não pretendo dizer-lhe como fazê-lo. Se você estiver interessado no método que eu hackeei, você encontrará no código.
Uma vez calculadas as porcentagens de dano, elas são apresentadas aos jogadores. Por exemplo, se apenas o navio na posição 2 foi atingido e tem 50% de dano, isso seria mostrado como.
? ?
|\ /|
| \ / |
| \ / |
| 50% |
| / \ |
| / \ |
|/ \|
? ?
O jogo continua a pedir bombas e executar o cenário até que um jogador tenha perdido todos os seus navios. Nesse ponto, o outro jogador ganha.
Você pode notar que bombardear o terceiro navio de um jogador causa um dano de cerca de 25%. Como esse navio é um terço do caminho para a destruição, você poderia esperar 33%. O motivo é trigonometria. Não há necessidade de insistir muito sobre isso neste momento.
É importante notar que todo o cenário é repetido todas as vezes. Se a quantidade de tempo entre os turnos pode ser apenas cerca de um minuto, mas isso é quase uma eternidade para os qubits. Mesmo a uma temperatura de 0,02 Kelvin, a informação teria queimado muito antes do próximo turno. Além disso, nossa necessidade de extrair informações também irá perturbar toda a adorável quantumidade do sistema. Por essas razões, qualquer processo que necessite de interação humana, precisará das partes quânticas a serem reexecutadas do zero para cada nova entrada.
Então foi isso. Battleships rodando em um computador quântico. Não é o uso mais requintado de um computador quântico, ou a versão mais extravagante de Battleships. Mas para mim, combinar os dois é metade da diversão!
O código fonte completo pode ser acessado abaixo.
E aqui está um vídeo do jogo em ação.
A história continua com outra versão do Battleships na parte 2.
Autor: Dr. James Wootton
