Como programar um computador quântico - Parte 2
Navios de guerra com medições quânticas

Este artigo tem “Parte 2” no título por um bom motivo. Havia uma Parte 1, na qual analisamos a base para escrever e executar programas quânticos.
Eu vou assumir que você leu pelo menos a primeira metade antes de vir aqui.
A maior parte do conhecimento real de codificação necessário para este tutorial foi abordado na última vez. Este artigo se concentrará principalmente em algumas das coisas que podemos fazer com esses comandos.
Como olhar para qubits
Nos programas, temos variáveis. Em algum momento, precisaremos olhar para eles.
Isso pode ser no final do programa quando obtivermos o resultado. Também pode ser durante o programa, quando usamos a variável como parte de uma instrução condicional. De qualquer maneira, isso acontece muito. E ao programar variáveis não quânticas, é um processo bastante normal.
Isso ocorre porque variáveis não quânticas têm valores definidos. Olhá-los apenas nos diz, ou outras partes do programa, qual é o valor. Nada sobre a variável em si mudará.
Isso não se aplica às variáveis quânticas, que podem ter valores indefinidos. Eles podem estar na chamada superposição quântica, o que lhes permite manter múltiplos valores contraditórios ao mesmo tempo.
Quando olhamos para eles, eles têm que desistir de toda essa estranheza. Eles são forçados a assumir um valor definido e depois nos dizem qual é esse valor. Como este não é apenas um processo passivo, ele precisa ser cuidadosamente considerado. E precisa de um nome. Nós chamamos isso de medição.
Neste artigo, exploraremos algumas das propriedades da medição. Também vamos usá-lo como base de uma mecânica de jogo e ver exatamente como programá-lo em um computador quântico. No final, teremos uma nova versão do encouraçado.
Mapeando o mundo de um qubit
Antes de realmente começarmos a medir qubits, devemos tentar entender um pouco mais o mundo deles. A melhor maneira de visualizar um qubit é usando uma esfera. Qualquer estado de qubit possível corresponde a um ponto na superfície dessa esfera.
Os estados 0 e 1 são completamente diferentes, completamente disjuntos. Eles são os opostos um do outro. Eles viverão, portanto, em lados opostos da esfera. Geralmente escolhemos colocar 0 no polo norte e 1 no sul.
Vamos escolher um ponto equidistante entre os dois, em algum lugar ao longo do equador. Pode estar em qualquer lugar que você quiser. Vamos chamá-lo de +. Por que + ? Por que não?
O estado + também tem um oposto, tão diferente quanto 0 é de 1. Isso vive no lado oposto, que também será um ponto ao longo do equador. Vamos chamar esse estado - .
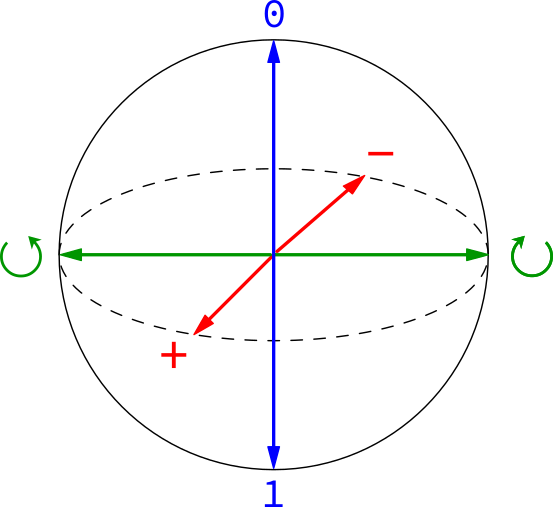
Com os pontos 0, 1, + e - agora definidos, mais alguns pontos estão implorando por nossa atenção. Estes são os que são equidistantes entre 0 e 1 e também são equidistantes entre + e -. Vamos chamar isso de ↻ e ↺. Por quê? Porque uma vez vi um cara que não escreveu o Código Da Vinci fazendo isso e gostei.
Agora, mapeamos o mundo do qubit com seis pontos. Estes não são de forma alguma os únicos que jamais usaremos. Eles são simplesmente os marcos pelos quais navegaremos.
Medindo um qubit
Qualquer medida é simplesmente pedir um qubit para escolher entre dois pontos opostos na esfera.
O exemplo clássico é para o nosso par favorito de estados opostos: 0 e 1. Pedimos ao qubit para escolher entre os dois. Se já estava no estado 0, será 0. O qubit no estado 1 fornecerá o resultado 1. Da mesma forma, para qualquer outro estado, o resultado será aleatório, sendo a opção mais próxima a mais provável.
No equador, há uma chance de 50/50 de qualquer maneira. Portanto, se nosso estado foi + ou - e perguntamos se é 0 ou 1, ele terá que escolher um ou outro com igual probabilidade.
A medida baseada em 0 e 1 tem alguns nomes. Podemos chamá-lo de uma medida 0/1, por razões óbvias. Também é chamada de medição da base Z, devido à relação especial que os estados 0 e 1 têm com uma operação chamada z. Mais sobre essa história outra vez.
O próximo tipo de medição mais popular é o de + e -. Chamaremos isso de medida +/-, mas você também pode chamar de medida base X.
Funciona da mesma maneira que antes, mas apenas para + e - em vez de 0 e 1. Portanto, se você começar com um qubit no estado + e fizer essa medição, obterá o resultado +. Mas se você começar com 0 e fizer a mesma pergunta, ele escolherá aleatoriamente.
Também temos uma medida para as coisas estranhas das flechas. Isso é chamado de medida de base Y. Ninguém gosta de medições com base em Y.
Um bit é apenas um bit, mesmo quando é quântico
A medição de objetos não quânticos é um processo passivo. Ele informa o que o objeto está fazendo, mas não o altera de forma alguma.
Medir coisas quânticas é muito diferente. As medidas quânticas não mudam apenas nosso conhecimento sobre as variáveis. Eles mudam as próprias variáveis.
Suponha que você tenha um qubit no estado + e pergunte se é 0 ou 1. Quando ele fornece um resultado aleatório, ele não está apenas enganando você. Não está dizendo nada a você, porque você fez a pergunta errada. Uma vez que você obtiver um resultado, ele permanecerá com ele. O valor será alterado para refletir a resposta. Se ele indicar 0, será 0 para sempre (ou até você mexer com ele novamente, pelo menos). Esquecerá que sempre foi +.
Isso significa que um qubit só pode ter certeza de seu resultado em uma única medição. Se souber definitivamente se é 0 ou 1, é completamente incerto se é + ou - e também completamente incerto se é ↻ ou ↺. Um qubit tem apenas uma quantidade limitada de certeza, limitada pelo princípio da incerteza de Heisenberg.
Isso significa que apenas conseguimos obter informações de um qubit. Depois que extraímos um único resultado binário, tudo o que o qubit sabia antes da medição é esquecido. Apenas lembra o resultado que nos deu. E assim, apesar do número infinito de possíveis estados de qubit, só podemos extrair um único bit de informação. É por isso que pensamos nisso como a versão quântica de um bit, em vez de um float quântico ou vetor quântico 3, etc.
A mecânica do jogo
Vamos fazer uma variante de encouraçados na qual haverá dois tipos de ataque: bombas e torpedos. Apenas um ataque bem-sucedido será necessário para afundar um navio, mas nem sempre é fácil obter um ataque bem-sucedido. Alguns navios têm uma defesa tão grande contra aeronaves que nenhuma bomba chegará perto deles. Outros são ótimos em repelir torpedos.
Para implementar isso em um computador normal, poderíamos definir duas variáveis booleanas para cada navio. Um nos diria se o navio é imune a bombas e o outro a torpedos. Eles podem ser verificados durante os ataques para ver se o navio afunda ou não.
Se essa fosse a implementação que usamos, teoricamente seria possível que um navio estivesse imune a ambos os tipos de ataque. Isso seria um design de jogo ruim, pois torna impossível a vitória de um jogador. Uma boa implementação precisaria impedir a existência de navios indestrutíveis.
Uma maneira de evitar criar esses navios é com algumas linhas simples de código. Esse não é realmente o nosso estilo, no entanto. Em vez disso, vamos corrigi-lo com a mecânica quântica!
Especificamente, tentaremos espremer esses dois booleanos em um único qubit. Como eles não se encaixam, teremos um comportamento quântico interessante. Isso adicionará uma jogabilidade interessante ao jogo, além de impedir que qualquer nave seja indestrutível.
Implementaremos isso associando um ataque a bomba com uma medida 0/1. Se obtivermos o resultado 1, dizemos que o navio afundou. Para 0, deduzimos que o navio é imune a ataques a bomba. Para torpedos, fazemos uma medição +/-, com - implicando destruição e + imunidade. Esse método torna impossível que um navio seja definitivamente imune aos dois tipos de ataque. Se descobrirmos que uma nave inimiga é imune a bombas (ou seja, seu estado é 0), sabemos que deve ser completamente incerto sobre torpedos (o resultado de uma medição +/-). Como um ataque a bomba certamente falharia, deveríamos atacar com torpedos a seguir.
Pode acontecer que o ataque do torpedo falhe (o estado se torna + após a medição +/-). O navio decidirá que é definitivamente imune a eles, e qualquer outro ataque de torpedo falhará. Mas toda a esperança não está perdida. Ao se certificar de torpedos, tornou-se incerto sobre bombas. Atacar com eles a seguir (fazer uma medição de 0/1) pode levar à vitória.
Se o ataque às bombas não der certo, voltamos aos torpedos e assim por diante. A melhor tática é continuar alternando entre os dois até o navio finalmente afundar.
Começaremos os navios como incertos sobre sua imunidade aos dois ataques. Isso pode ser feito inicializando o qubit em um dos estados da base Y. Vamos para ↻. Este é realmente um estado que encontramos na Parte 1, ou seja, u3 (0,5 * pi, 0,0) 0, portanto já sabemos como fazê-lo.
Lidando com qubits de vida curta
Implementar o jogo em um processador quântico não será tão fácil quanto poderíamos esperar. Vamos dar uma olhada em todos os problemas que surgirão no nosso caminho e ver como contorná-los.
Suponha que um navio seja atacado por uma bomba e sobreviva. Então, na próxima rodada, ele é atingido por um torpedo.
Se o jogo foi executado em um computador normal e foi simulado usando bits normais, a implementação disso seria bastante simples. O navio seria inicializado quando o jogo começar e, então, espere na memória até que o jogador decida o que fazer com ele. Uma vez que o jogador envia uma bomba, as operações correspondentes serão aplicadas para ver se ela é destruída. Se sobreviver, aguarda novamente até o próximo ataque.
Isso não vai funcionar para nós. Os Qubits não podem ficar esperando a escala de tempo humana. Alguns segundos são tempo mais do que suficiente para eles travarem e queimarem, pelo menos com a tecnologia atual.
A alternativa é executar um novo processo quântico toda vez que um ataque é feito. O primeiro trabalho será inicializado com o estado,, para que os resultados sejam aleatórios para uma medição 0/1 (ataque a bomba) ou uma medição +/- (ataque a torpedo). O resultado da medição é então gravado e armazenado na memória no computador normal. Quando o próximo ataque acontece, outro trabalho é criado para ver o que acontece. Será inicializado com o resultado da última medição e, portanto, continuará.
Fazendo uma medição +/-
Até o momento, escrevi uma grande quantidade de palavras, mas não uma única linha de código. Vamos começar lembrando como uma medição 0/1 é implementada no código QASM.
measure q[0] -> c[0];
O papel de c[0] aqui é importante revisitar. É a saída do processo de medição. É o bit normal em que o resultado da medição é armazenado. Para uma medição 0/1, o resultado é 0 ou 1.
Tudo isso é bastante simples para uma medição 0/1. Mas são as medidas +/- que estamos vendo agora. Como extraímos as informações de um deles?
Ainda queremos armazenar o resultado em um bit normal c[0]. Por ser um pouco normal, não tem conhecimento dos estados estranhos + e -. Ele conhece apenas o binário normal. Optamos, portanto, por reportar o resultado + como c[0] = 0 e - como c[0] = 1. O fato de parecerem iguais aos resultados de uma medição 0/1 não será um problema. Como em qualquer programa de computador, devemos saber o que programamos e, portanto, saber como interpretar os resultados.
Agora sabemos como obter os resultados de uma medição +/-. Mas ainda não descobrimos como fazer uma. Isso ocorre porque precisamos ser sorrateiros sobre isso. Precisamos hackear o processo que faz medições 0/1 e, em vez disso, fizemos uma +/-.
A chave para o nosso hack é uma operação chamada Hadamard. A aplicação disso a um qubit q[0] no código QASM se parece com isso.
h q[0];
O comando que usamos no Python para adicionar essa linha a um arquivo QASM chamado gridScript é
gridScript.h(q[0])
O efeito do Hadamard é trocar estados de base Z por estados de base X e vice-versa. É uma rotação da Esfera que move o estado qubit de 0 para um + e + para 0. Da mesma forma, 1 é girado para - e vice-versa.
Isso significa que a história que podemos contar sobre um qubit em termos de 0 e 1 antes do Hadamard, é preciso contar com + e - depois dele. E qualquer história de + e - se torna uma de 0 e 1.
É exatamente disso que precisamos. Isso significa que uma medição +/- em um qubit q[0] pode ser feita pelo seguinte código QASM.
h q[0];
measure q[0] -> c[0];
h q[0];
Para ver por que isso funciona, vamos ver alguns exemplos. O qubit q[0] começará recentemente declarado em cada um e, portanto, estará em seu valor inicial padrão de 0.
Exemplo Zero:
measure q[0] -> c[0];
O qubit começa no estado 0. É perguntado se é 0 ou 1 e diz a c[0] a resposta. O resultado será sempre c[0] = 0.
Exemplo Um
x q[0];
measure q[0] -> c[0];
O qubit começa no estado 0 e, em seguida, é rotacionado para 1. Em seguida, é perguntado se é 0 ou 1. Ele sempre responde 1.
Exemplo +:
h q[0];
measure q[0] -> c[0];
O qubit começa no estado 0 e é rotacionado imediatamente para +. É então perguntado se seu estado é 0 ou 1. Ele escolhe aleatoriamente um ou outro, e seu estado é atualizado com a resposta. Agora, fizemos alguns exemplos triviais, vamos fazer algo mais complexo.
Exemplo ++:
h q[0];
h q[0];
measure q[0] -> c[0];
h q[0];
O qubit começa no estado 0 e depois é rotacionado para +. Depois disso, existem duas maneiras equivalentes pelas quais podemos continuar a história.
Uma é dizer que as três linhas finais coletivamente fazem uma medida +/-. Eles perguntam ao qubit se é + ou -. Para + eles retornam o resultado c [0] = 0 e para - eles retornam c [0] = 1. Como o qubit entra na medição com o estado + neste exemplo, é sempre medido como um +. Portanto, sai da medição ainda neste estado.
Para a outra história, examinamos os efeitos das linhas, um por um. O segundo Hadamard desfaz o efeito do primeiro e, portanto, gira o qubit de volta ao estado 0. É então perguntado se seu estado é 0 ou 1 e, portanto, sempre responde a 0. Um outro Hadamard o gira novamente para +.
Ambas as histórias concordam com os efeitos observáveis. Eles concordam que a saída c [0] sempre será 0 e concordam que o estado qubit no final será +. Eles simplesmente discordam de como isso aconteceu. Ambas as interpretações são igualmente válidas.
Se você deseja que algum jargão procure as coisas na Wikipedia, estes são exemplos das imagens de Schrödinger e Heisenberg da mecânica quântica.
Exemplo +1:
x q[0];
h q[0];
measure q[0] -> c[0];
h q[0];
Aqui está outro exemplo para o qual temos duas histórias equivalentes. Podemos dizer que q[0] começa como 0 e depois é rotacionado para 1. Isso é rotacionado t0 - antes de passar pela medição 0/1. Ele decide aleatoriamente um ou outro, fornece a saída c[0] = 0 ou c[0] = 1 e atualiza seu estado de acordo. Se decidir 0, o Hadamard final o rodará para +. Caso contrário, terminará como -.
Alternativamente, poderíamos dizer que, depois de rotacionado para 1, o qubit passa por uma medição +/-. Ele decide aleatoriamente entre essas duas opções, fornecendo a saída c[0] = 0 para + e c[0] = 0 para -. O estado é atualizado de acordo, terminando no estado + ou -.
Novamente, essas duas histórias são igualmente válidas e concordam com todos os efeitos observáveis. Se queremos pensar nas três linhas
h q[0];
measure q[0] -> c[0];
h q[0];
como uma medida +/-, somos livres para fazê-lo. Se quisermos pensar nisso como um Hadamard seguido de uma medida 0/1 seguida por um Hadamard, tudo bem também.
Há uma coisa importante a ser observada antes de seguirmos em frente. Atualmente, a API da IBM não nos permite fazer nada com um qubit depois de medi-lo. Esta não é uma regra geral para computadores quânticos. Normalmente, esperamos poder continuar medindo e manipulando qubits pelo tempo que quisermos. Mas não podemos fazer isso no momento.
Isso não representa nenhum problema. Como os qubits não podem ficar parados enquanto os jogadores fazem escolhas de qualquer maneira, já temos que recriar completamente o estado após cada rodada de medição. O segundo Hadamard aparecerá efetivamente no próximo trabalho, atuando na versão reencarnada do estado.
Todas as outras medidas possíveis podem ser obtidas por hacks semelhantes. Nós apenas precisamos realizar algumas operações antecipadamente para indicar nossas medidas alternativas e, em seguida (se a API permitir), realizar as operações opostas logo após.
Lidando com erros
A tecnologia quântica atual não é perfeita. Os qubits nem sempre fazem o que deveriam. Se seu qubit é 0 e você faz uma medição 0/1, o resultado deve sempre ser 0. Sempre. Mas com os dispositivos quânticos atuais, há uma chance de ser 1. Pode ser porque uma operação x se infiltrou enquanto não estávamos olhando. Pode ser porque a medida está mentindo para nós. Eventos como esses são raros, mas acontecem. Existem duas maneiras de lidar com os erros. Um é ignorá-los. Podemos escrevê-los na narrativa do jogo. Há grandes tempestades no mar.
Isso às vezes leva um navio a ser destruído por um ataque, mesmo que seja imune. Ou sobreviver a um ataque que deveria ter destruído. A segunda maneira de lidar com os erros é tentar remover seus efeitos. Se muitos qubits estivessem disponíveis, poderíamos fazer isso com correção quântica de erros. Infelizmente, ainda faltam alguns anos.
Em vez disso, faremos algumas estatísticas. Para isso, precisamos de probabilidades, que conseguimos executando cada trabalho muitas vezes e vendo com que frequência cada resultado possível aparece.
No caso silencioso, as probabilidades seriam todas de 0%, 100% ou 50%. Um resultado é impossível (como obter um 1 se o estado for 0), certo (como obter um + se o estado for +) ou completamente aleatório (como obter um 0 quando o estado é +).
O barulho vai atrapalhar um pouco. Quando fazemos uma medição 0/1 de um 0, podemos descobrir que o resultado 0 ocorre apenas 98% das vezes, com 2% indo para 1. Para corrigir isso, faremos algo bastante arbitrário. Decidiremos que algo com menos de 5% de probabilidade nunca deveria ter acontecido. Qualquer coisa com mais de 95% de probabilidade deveria ter sido certa.
Juntando tudo
Este artigo abordou os traços gerais da mecânica do jogo para esta versão do Battleships e como implementá-lo com um computador quântico. Em vez de examinar todos os detalhes detalhados aqui, deixarei isso para os comentários no código-fonte real.
Quantum Battleships with complementary measurements
"\n",
"print(\"\\n\\n\\n\\n\\n\\n\\n\\n\")\n",
"print(\" ██████╗ ██╗ ██╗ █████╗ ███╗ ██╗████████╗██╗ ██╗███╗ ███╗ \")\n",
"print(\" ██╔═══██╗██║ ██║██╔══██╗████╗ ██║╚══██╔══╝██║ ██║████╗ ████║ \")\n",
"print(\" ██║ ██║██║ ██║███████║██╔██╗ ██║ ██║ ██║ ██║██╔████╔██║ \")\n",
"print(\" ██║▄▄ ██║██║ ██║██╔══██║██║╚██╗██║ ██║ ██║ ██║██║╚██╔╝██║ \")\n",
"print(\" ╚██████╔╝╚██████╔╝██║ ██║██║ ╚████║ ██║ ╚██████╔╝██║ ╚═╝ ██║ \")\n",
"print(\" ╚══▀▀═╝ ╚═════╝ ╚═╝ ╚═╝╚═╝ ╚═══╝ ╚═╝ ╚═════╝ ╚═╝ ╚═╝ \")\n",
"print(\"\")\n",
"print(\" ██████╗ █████╗ ████████╗████████╗██╗ ███████╗███████╗██╗ ██╗██╗██████╗ ███████╗\")\n",
"print(\" ██╔══██╗██╔══██╗╚══██╔══╝╚══██╔══╝██║ ██╔════╝██╔════╝██║ ██║██║██╔══██╗██╔════╝\")\n",
"print(\" ██████╔╝███████║ ██║ ██║ ██║ █████╗ ███████╗███████║██║██████╔╝███████╗\")\n",
"print(\" ██╔══██╗██╔══██║ ██║ ██║ ██║ ██╔══╝ ╚════██║██╔══██║██║██╔═══╝ ╚════██║\")\n",
"print(\" ██████╔╝██║ ██║ ██║ ██║ ███████╗███████╗███████║██║ ██║██║██║ ███████║\")\n",
"print(\" ╚═════╝ ╚═╝ ╚═╝ ╚═╝ ╚═╝ ╚══════╝╚══════╝╚══════╝╚═╝ ╚═╝╚═╝╚═╝ ╚══════╝\")\n",
"print(\"\")\n",
"print(\" ___ ___ _ _ \")\n",
"print(\" | _ ) _ _ | \\ ___ __ ___ __| | ___ | |__ _ _ \")\n",
"print(\" | _ \\| || | | |) |/ -_)/ _|/ _ \\/ _` |/ _ \\| / /| || |\")\n",
"print(\" |___/ \\_, | |___/ \\___|\\__|\\___/\\__,_|\\___/|_\\_\\ \\_,_|\")\n",
"print(\" |__/ \")\n",
"print(\" James Wootton, University of Basel\")\n",
"print(\"\")\n",
"print(\" A game played on a real quantum computer!\")\n",
"print(\"\")\n",
"print(\" Learn how to make your own game for a quantum computer at decodoku.com\")\n",
"print(\"\")\n",
"print(\"\")\n",
"randPlace = input(\"> Press Enter to start...\\n\").upper()"
Autor: Dr James Wootton