Criptografia Homomórfica para Iniciantes - Um Guia Prático (Parte 2 | A Transformação Fourier)
Criptografia Homomórfica para Iniciantes: Um Guia Prático (Parte 2: A Transformação Fourier)
Na parte 1 deste guia, cobrimos muitos dos fundamentos da criptografia homomórfica. Na Parte 2, discutiremos uma aplicação prática da criptografia homomórfica ao processamento de sinais que preserva a privacidade. Para aqueles de vocês que não têm interesse em processamento de sinal, fique ligado na Parte 3 do guia, o que deve ser útil para um público mais geral.
O objetivo deste post é duplo: 1) demonstrar que o processamento de sinal no domínio criptografado pode realmente ser bastante prático e 2) fornecendo uma visão geral de alguns dos códigos escritos para o professor Gerald Penn e meu artigo para o Interspeech 2019 intitulado “Extraindo Coeficientes Cepstral de Frequência de Mel e Casca de Sinais Criptografados”.
Transformação fourier discreta real
A Fourier Transform (FT) é uma das operações mais fundamentais no processamento de sinais. Ele leva um sinal do domínio do tempo para o domínio de frequência. Se você precisar de uma cartilha para ft, uma das explicações mais claras que eu encontrei até agora está em “Um Guia de Um Estudante para Ondas”. Se você não pode colocar as mãos nesse livro, existe uma quantidade abundante de descrições online.
Agora, para aqueles que já estão familiarizados com ft, você pode estar se perguntando como podemos converter a seguinte fórmula para o domínio criptografado:

Fonte: https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
Bem, não usaremos a fórmula padrão ft, já que significaria ter que lidar com a complexidade adicional da contabilidade de números imaginários dentro de cálculos criptografados. Em vez disso, usaremos as fórmulas do Real Discrete Fourier Transform (RDFT), que são muito bem descritas em [1]:

Fonte: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1164632
onde N é o número de amostras, x(·) é o vetor representando o sinal, e
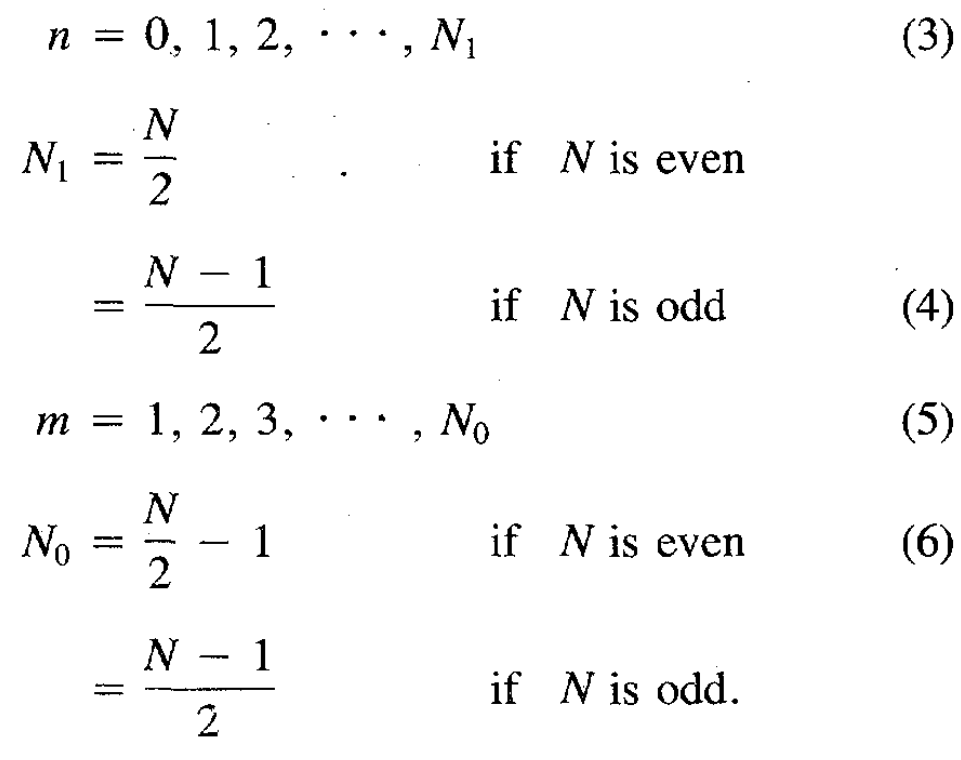
Fonte: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1164632
Para calcular o RDFT, adicionamos a Discreta Transformação cossina (DCT) com a Discreta Transformação do Sine (DST). Para simplificar, referimos-nos à versão criptografada de valores ∗ como E(∗).
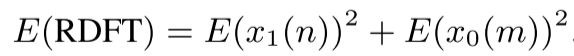
Felizmente para nós, cos (2πnk/N) e sin(2πmk/N) podem ser pré-computadorados e não precisam ser criptografados antes de multiplicar os valores com o sinal criptografado. Preparamos esses valores para uso com o esquema de criptografia homomórfica B/FV da Biblioteca de Criptografia de Treliça PALISADE. Note que precisamos escolher uma precisão para arredondar os valores pelos quais multiplicaremos nosso sinal. Escolhemos o número de casas decimais a serem retidas com base em um nível de precisão desejado φ, em seguida, multiplicamos os dados por 10^φ (usamos ^ para significar “para o poder de”) e redondo para o inteiro mais próximo.
Vamos trabalhar as pré-compensações primeiro. Para o DCT, temos que calcular:

Codificamos a seção destacada da seguinte forma:
Plaintext calculate_cosine_array(int n, int N, int start, int stop, CryptoContext<DCRTPoly> cc) {
vector<int64_t> *cosines = new vector<int64_t>();
for (int k = 0; k != N; k++) {
if (k < start || k >= stop) {
cosines->push_back(0);
continue;
}
int cosVal = int(cos(((2 * pi * k * n) / N)) * 100); //FOR MORE ACCURATE RESULTS, INCREASE MULTIPLE OF 10
cosines->push_back(cosVal);
}
Plaintext cosineArray = cc->MakePackedPlaintext(*cosines);
return cosineArray;
}
Realizamos cálculos quase idênticos para o DST.

Codificamos a seção destacada da seguinte forma:
Plaintext calculate_sine_array(int m, int N, int start, int stop, CryptoContext<DCRTPoly> cc) {
vector<int64_t> *sines = new vector<int64_t>();
for (int k = 0; k != N; k++) {
if (k < start || k >= stop) {
sines->push_back(0);
continue;
}
int sinVal = int(sin(((2 * pi * k * m) / N)) * 100); //FOR MORE ACCURATE RESULTS, INCREASE MULTIPLE OF 10
sines->push_back(sinVal);
}
Plaintext sineArray = cc->MakePackedPlaintext(*sine);
return sineArray;
}
Espero que essas pré-recompensas sejam bastante autoexplicativas.
Em seguida, precisamos criptografar o sinal. Para nossos experimentos, usamos uma gravação de áudio de uma conversa telefônica do corpus switchboard. O tipo de sinal só é relevante aqui na medida em que se conhece a taxa de amostra, que é de 8kHz. Caso precisemos fazer divisão, criamos uma estrutura de frações para armazenar números criptografados. Embora isso não seja útil para os cálculos rdft, é necessário calcular Coeficientes Cepstral (que é o tema do papel para o qual este código foi originalmente escrito).
struct CryptoFractions {
Ciphertext<DCRTPoly> encryptedNumerators;
Ciphertext<DCRTPoly> encryptedDenominators;
vector<int64_t> numerators;
vector<int64_t> denominators;
};
Criptografamos o sinal da seguinte forma:
CryptoFractions encrypt_audio(vector<float> signal, int startIndex, int sampleSize, const char *keysFilePath, const long precision) {
vector<int64_t> intSignal;
CryptoFractions encryptedSignal;
int numerator;
int endIndex = startIndex + sampleSize;
for (int i = startIndex; i < endIndex; i += 1) {
numerator = int(signal[i] * precision);
encryptedSignal.numerators.push_back(numerator);
encryptedSignal.denominators.push_back(1);
}
int val;
EncryptionInfo info = read_encryption_info(keysFilePath);
Plaintext signalArray = info.cryptocontext->MakePackedPlaintext(encryptedSignal.numerators);
Plaintext ones = info.cryptocontext->MakePackedPlaintext(encryptedSignal.denominators);
Ciphertext<DCRTPoly> encSignal = info.cryptocontext->Encrypt(info.keypair.publicKey, signalArray);
// For now, the denominator will be 1. We keep track of the precision adjustments separately and deal with that once we are ready to decrypt the result
Ciphertext<DCRTPoly> encSignalDen = info.cryptocontext->Encrypt(info.keypair.publicKey, ones);
encryptedSignal.encryptedNumerators = encSignal;
encryptedSignal.encryptedDenominators = encSignalDen;
return encryptedSignal;
}
Agora finalmente temos as ferramentas necessárias para calcular o RDFT:
/*N is signal size (number of samples), sampleRate in kHz (num samples per ms), frameLength in ms, shiftLength in ms*/
vector<vector<Ciphertext<DCRTPoly>>> real_discrete_fourier_transform(int N, int sampleRate, int frameLength, int shiftLength, CryptoContext<DCRTPoly> cc, LPPublicKey<DCRTPoly> publicKey, CryptoFractions encSignal, LPPrivateKey<DCRTPoly> sk) {
int boundN, boundM;
if (N % 2 == 0) {
boundM = N / 2 - 1;
boundN = N / 2;
}
else {
boundM = (N - 1) / 2;
boundN = (N - 1) / 2;
}
vector<int64_t> zeros = { 0 };
vector<int64_t> one = { 1 };
for (int i = 0; i < frameLength - 1; i += 1) {
zeros.push_back(0);
one.push_back(0);
}
Plaintext zerosPT1 = cc->MakePackedPlaintext(zeros);
Plaintext zerosPT2 = cc->MakePackedPlaintext(zeros);
Plaintext onePTRe = cc->MakePackedPlaintext(one);
Plaintext onePTIm = cc->MakePackedPlaintext(one);
Ciphertext<DCRTPoly> zerosCT1;
Ciphertext<DCRTPoly> zerosCT2;
Ciphertext<DCRTPoly> oneCTRe;
Ciphertext<DCRTPoly> oneCTIm;
zerosCT1 = cc->Encrypt(publicKey, zerosPT1);
zerosCT2 = cc->Encrypt(publicKey, zerosPT2);
oneCTRe = cc->Encrypt(publicKey, onePTRe);
oneCTIm = cc->Encrypt(publicKey, onePTIm);
int numSamplesInFrame = sampleRate * frameLength;
int numSamplesInShift = sampleRate * shiftLength;
unsigned long batchSize = upper_power_of_two(numSamplesInFrame);
Plaintext cosines;
Plaintext sines;
Ciphertext<DCRTPoly> innerProductRe;
Ciphertext<DCRTPoly> innerProductIm;
Ciphertext<DCRTPoly> resultRe;
Ciphertext<DCRTPoly> resultReSquared;
Ciphertext<DCRTPoly> resultIm;
Ciphertext<DCRTPoly> resultImSquared;
Ciphertext<DCRTPoly> resultRDFT;
vector<vector<Ciphertext<DCRTPoly>>> resultsRe = vector<vector<Ciphertext<DCRTPoly>>>(int(ceil(float(N) / float(numSamplesInShift))));
vector<vector<Ciphertext<DCRTPoly>>> resultsIm = vector<vector<Ciphertext<DCRTPoly>>>(int(ceil(float(N) / float(numSamplesInShift))));
vector<vector<Ciphertext<DCRTPoly>>> RDFT = vector<vector<Ciphertext<DCRTPoly>>>(int(ceil(float(N) / float(numSamplesInShift))));
int atFrame = 0;
resultsIm[atFrame].push_back(zerosCT1);
for (int i = 0; i <= N; i += numSamplesInShift) {
for (int n = 0; n <= boundN; n++) {
// CALCULATE DCT
cosines = calculate_cosines(boundN, n, N, i, i + numSamplesInFrame, cc, publicKey);
innerProductRe = cc->EvalInnerProduct(encSignal.encryptedNumerators, cosines, batchSize);
resultRe = cc->EvalMult(innerProductRe, oneCTRe);
resultsRe[atFrame].push_back(resultRe);
resultReSquared = cc->EvalMult(resultRe, resultRe);
//CALCULATE DST
if ((n + 1) <= boundM) {
sines = calculate_sines(boundM, n + 1, N, i, i + numSamplesInFrame, cc, publicKey);
innerProductIm = cc->EvalInnerProduct(encSignal.encryptedNumerators, sines, batchSize);
resultIm = cc->EvalMult(innerProductIm, oneCTIm);
resultsIm[atFrame].push_back(resultIm);
resultImSquared = cc->EvalMult(resultIm, resultIm);
}
else if ((n + 1) == boundM+1) {
resultsIm[atFrame].push_back(zerosCT2);
}
resultRDFT = cc->EvalAdd(resultReSquared, resultImSquared);
RDFT[atFrame].push_back(resultRDFT);
}
atFrame += 1;
}
return RDFT;
}
Desempenho
Para um nível de segurança de 128 bits, é preciso 46,5235 s para calcular os RDFTs de 100 quadros, dada uma taxa de amostra de 16, um comprimento de quadro de 25 e um comprimento de mudança de 10 em uma CPU Intel Core i-7-8650U @ 1.90GHz e uma RAM de 16 GB.
Esses cálculos são, naturalmente, paralelosizáveis. Se fôssemos executar este código em um dispositivo mais poderoso e fosse até mesmo para adaptá-lo às GPUs, poderia se tornar bastante prático para executar FTs criptografados na nuvem.
Para que podemos usar isso?
Muitas vezes, a saúde é o primeiro setor que vem à mente quando se discute coleta e processamento de dados sensíveis. Gravações de áudio da voz de um paciente podem realmente conter um monte de informações que são úteis para diagnosticar doenças (grite para winterlight labs, professor Frank Rudzicz, e Dr. Katie Fraser que fizeram um grande trabalho no uso do processamento da fala para detectar prejuízos cognitivos como demência).
Um método para detectar vozes patológicas é calcular o nervosismo, que mede se um gesto é sustentado durante um curto período de tempo [2].
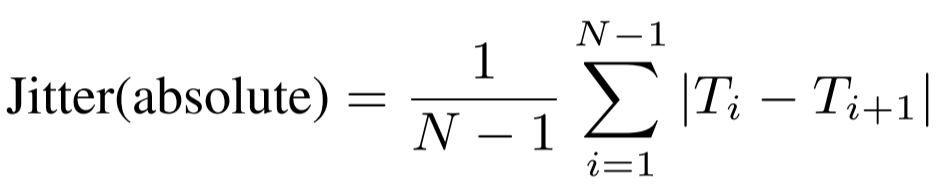
T_i ( _ usado para significar subscrito) são os comprimentos de período de frequência fundamental extraído (F_0) e N é o número de períodos de F_0 extraídos [3].
Além da fala, as imagens são outro tipo de sinal que pode conter amplas informações confidenciais. A Transformação Fourier é frequentemente usada no processamento de imagens (por exemplo, para filtragem de imagens).
Agradecimentos
Este trabalho foi apoiado por uma Bolsa de Pós-Graduação da RBC e o BRAIN Ontario Research Fund.
Sinta-se livre para me enviar um e-mail no pthaineATcsDOTutorontoDOTedu se você quiser conversar sobre processamento de sinal criptografado.
Referências
[1] O. Ersoy, “Real Discrete Fourier Transform”, IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 33, no. 4, pp. 880-882, 1985.
[2] P. Perrot e G. Chollet, “Ajudando o Instituto de Pesquisa Forense da Gendarmerie Francesa a identificar um suspeito na presença de disfarce de voz ou falsificação de voz”, no Reconhecimento forense do orador. Springer, 2012, pp. 469-503.
[3] M. Farrus, J. Hernando e P. Ejarque, “Medidas de Jitter e Shimmer para reconhecimento de palestrantes”, na Oitava Conferência
Anual da Associação Internacional de Comunicação de Fala, 2007.
Autor: Patrícia Thaine