Números co-primos

Números coprimossão pares de números que não têm nenhum fator comum além de 1. Deve haver um mínimo de dois números para formar um conjunto de números co-primos. Tais números têm apenas 1 como seu maior fator comum, por exemplo, (4 e 7), (5, 7, 9) são números co-primos. Deve-se notar que os números co-primos não precisam ser números primos sempre. Dois números compostos como 4 e 9 também formam um par deco-primos.

O que são Números Co-primo?

Se o únicofatorcomum de dois números a e b é 1, então a e b são números coprimos. Neste caso, (a, b) é dito ser um par co-primo. Os números coprimos também são referidos como números relativamente primos.

Co primo Lista de Números

Dada abaixo está a lista de alguns co-primos para sua referência.

Pares de Números Co-primos
(2,15)
(3,8)
(4,9)
(5,6)
(11,14)
(15,19)

Como encontrar números co-primos?

Para descobrir se quaisquer dois números são co-primos, primeiro encontramos seuMaior Fator Comum (GCF). Se o seu GCF é 1, podemos dizer que eles são co-prime.

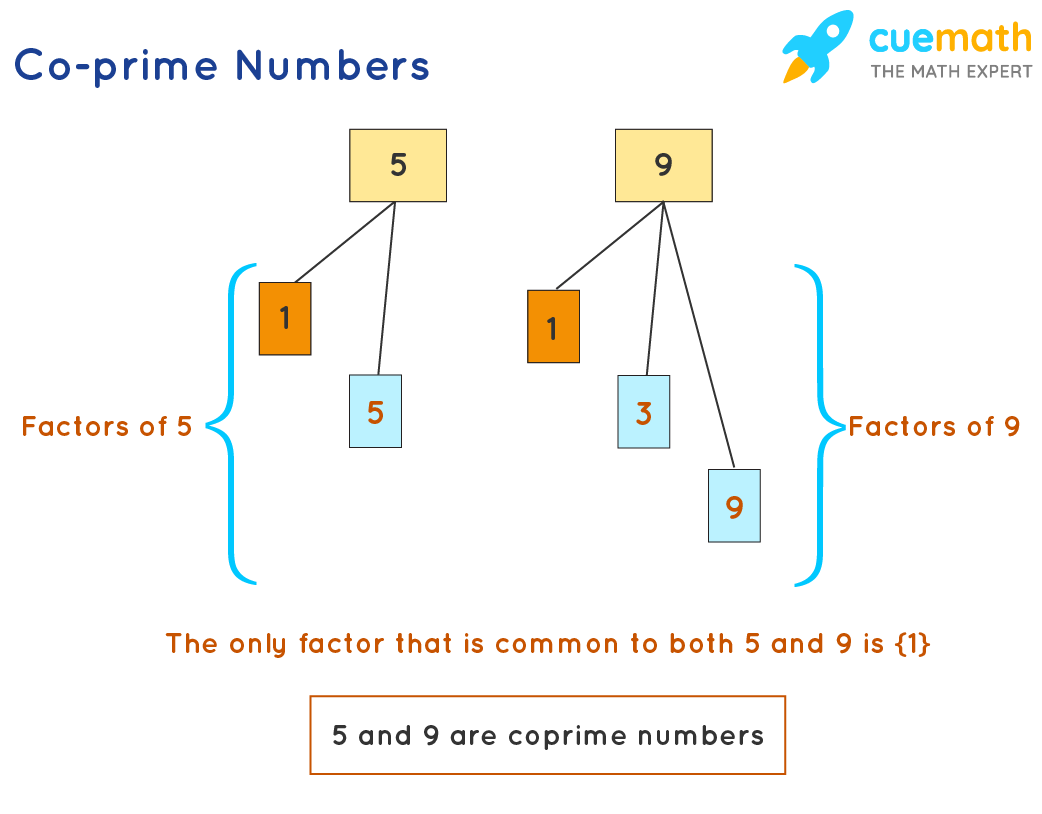
Exemplo 1: Consideremos dois números 5 e 9. Os fatores de 5 são 1 e 5. Osfatores de9 são 1, 3 e 9. O fator que é comum a 5 e 9 é 1. GCF de (5, 9) = 1. Assim, (5, 9) é um par co-primo.

Números co-primos

Exemplo 2: Consideremos dois números 6 e 10. Osfatores6 são 1, 2, 3 e 6. Os fatores de 10 são 1, 2, 5 e 10. Fatores que são comuns a 6 e 10 são 1 e 2. Assim, GCF (6, 10) = 2. Assim, (6, 10) NÃO é um par co-primo.

Exemplo de números coprimos

Propriedades dos números coprimos

Os números coprimos podem ser facilmente identificados com a ajuda de algumas propriedades que são explicadas abaixo:

  • OMaior Fator Comum (HCF) de dois números coprimos é sempre 1. Por exemplo,5 e 9 são números coprimos, lá, HCF (5, 9) = 1.
  • OMúltiplo Menos Comum (LCM) de dois coprimos é sempre o seu produto. Por exemplo, 5 e 9 são números co-primos. Assim, LCM (5, 9) = 45.
  • 1 forma um par de números co-primos com cada número.
  • Dois números pares não podem sernúmerosco-primos, pois sempre têm 2 como fator comum.
  • A soma de dois números co-primos é sempre co-primo com o seu produto. Por exemplo, 5 e 9 são números co-primos. Aqui, 5 + 9 = 14 é co-primo com 5 × 9 = 45.
  • Dois números primos são sempre co-primos. Eles têm apenas 1 como fator comum. Considere 29 e 31. 29 tem 2 fatores primos, 1 e 29 apenas. 31 tem 2 fatores primos, 1 e 31 apenas. 29 e 31 são números primos. Eles têm apenas um fator comum 1. Assim, eles são co-prime. Podemos verificar quaisquer dois números primos e obtê-los como co-primos. Por exemplo, 2 e 3, 5 e 7, 11 e 13, e assim por diante.
  • Todos os pares de doisnúmeros consecutivos são númerosco-primos. Quaisquer dois números consecutivos têm 1 como fator comum.

Considere alguns pares de tais números. Vamos tentar com 14 e 15.

Números1415
Fatores1,2,7,141,3,5,15
Fator comum1

Existem várias dessas combinações em que 1 é o único fator comum.

Números Co-prime e Twin Prime

Números coprimos são aqueles números cujo HCF é 1. Por outro lado, os números primos gêmeos são aqueles números primos cuja diferença é sempre 2. Por exemplo, 3 e 5 são números primos gêmeos. Os pontos a seguir listam a diferença entre os números primos coprimos e primos gêmeos.

  • Números primos gêmeos são sempre números primos, enquanto números coprimos também podem ser números compostos.
  • A diferença entre dois primos gêmeos é sempre 2, enquanto a diferença entre dois coprimos pode ser qualquer número.
  • Todos os pares de números primos gêmeos também são co-primos, enquanto todos os números coprimos podem ou não ser primos gêmeos.
  • 1 forma um par co-primo com cada número, enquanto forma um par primo gêmeo com apenas 3.

Co-primos Números 1 a 100

Na lista de números co-primos de 1 a 100, existem muitos pares que podem ser listados como números co-primos com base nas propriedades acima. Alguns dos pares de números coprimos que existem de 1 a 100 são (1, 2), (3, 67), (2, 7), (99, 100), (34, 79), (54, 67), (10, 11), etc. Tente formar mais desses pares de números co-primos por si mesmo. Aqui estáa calculadora co-prime on-line da Cuemathpara nossa facilidade.

Observações importantes:

  • Dois números são coprimos se o GCF for 1. Pode-se dizer também que, se o GCF de quaisquer dois números é 1, esses são números co-primos.
  • Os números coprimos não precisam necessariamente ser números primos. Por exemplo, 12 e 35 são números co-primos, embora, 12 e 35 NÃO sejam números primos.

Dicas e truques:

  • Quaisquer dois números primos são sempre co-primos.
  • Quaisquer dois números consecutivos são sempre co-primos.
  • 1 forma um par co-primo com qualquer outro número.
  • Um número primo é co-primo com qualquer outro número que não seja seu múltiplo.
  • Dois números pares NUNCA são co-primos.

☛ Tópicos relacionados

Artigo Original