A filosofia da programação
por Haoxian Chen
Raciocínio lógico === bom software
Photo by Giammarco Boscaro on Unsplash
A programação é a nova alfabetização. Mas como escrever bons programas? Aqui estão as questões recorrentes que precisamos resolver:
- Como chegar a soluções algorítmicas para um problema?
- Então, como sabemos que a solução realmente funciona?
- Mesmo que tenhamos certeza de que funciona, como dizemos ao computador para executá-lo?
Fato divertido – se você tem dificuldade em triturar qualquer uma dessas perguntas, você está realmente fazendo filosofia.
Para ver o porquê, vamos examinar algumas semelhanças interessantes entre programação e raciocínio filosófico.
O primeiro princípio: você tem que pensar muito.
Os computadores não fazem nada mais inteligente do que nós podemos fazer – a diferença é que eles fazem isso com velocidade mais rápida.
Mas eles não podem resolver um problema real como “como eu chego ao meu escritório de casa?”
Um método eficaz pode (em princípio) ser realizado por um ser humano sem a ajuda de qualquer maquinaria, exceto papel e lápis.
O mérito da programação ainda está na parte do raciocínio. Ou seja, traduzir um problema do mundo real em instruções simples que um computador pode executar.
É claro que diferentes linguagens de programação têm diferentes níveis de abstrações semânticas. Um programa Python pode ser mais curto do que seu equivalente C. Mas isso só muda a quantidade de traduções. Não podemos nos livrar do trabalho de tradução. Mas vamos deixar essa discussão para depois.
O fluxo de raciocínio de um programador
Agora estamos olhando para alguma descrição do problema. Podemos primeiro procurar exemplos de insumo-produto em pequena escala para entender o problema:
Indução. Precisamos de um algoritmo que possa lidar com esses exemplos. Agora você está fazendo indução: generalizando princípios a partir da experiência.
Dedução. Como saber se ele funciona para outras entradas desconhecidas? Fazemos dedução para provar a correção do nosso algoritmo.
Ontologia. Temos que manter os dados na memória do computador. O objetivo é torná-los eficientes para os computadores processarem. Em palavras de ordem, qual estrutura de dados pode capturar melhor o fluxo dinâmico das minhas informações?
Indução novamente. Depois vem a etapa final: a depuração. Induzimos a parte bugada do programa a analisar as saídas inesperadas.
Um exemplo
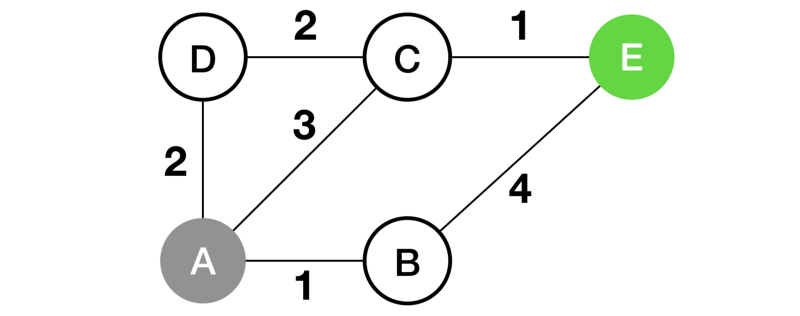
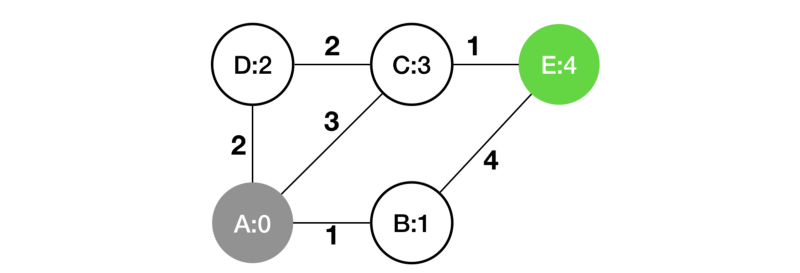
Agora vamos examinar o processo acima seguindo este exemplo real: encontrar o caminho mais curto do vértice A ao vértice E.
Um mapa simples. Os números denotam a distância da borda.
Para problemas de pequena escala, podemos resolvê-los por instintos. Tipo, é muito simples para nós reconhecer a solução A-C-E apenas olhando.
Mas e as topologias mais complexas? E quanto aos diferentes pesos de borda?
Precisamos da ajuda dos computadores. No entanto, não é simples dizer a um computador o que fazer. Há uma lacuna entre como os humanos pensam e como um computador funciona.
O processo
1. Generalizar princípios a partir da experiência: algoritmos
Para dizer a um computador o que fazer, precisamos primeiro criar um procedimento algorítmico.
Estratégias gananciosas são uma maneira natural de proceder. Ou seja, partindo do vértice A da fonte, e indo até o caminho mais curto conhecido. Continue explorando novos vértices até chegarmos ao destino E. E, de fato, essa abordagem satisfaz nosso exemplo.
A intuição é que, ao longo do caminho mais curto para um destino, cada nó intermediário é visitado no caminho mais curto também. (Claro que essa intuição pressupõe que todas as arestas têm pesos positivos. Isso pode não ser verdade, dependendo dos aplicativos. Discutiremos isso em detalhes mais adiante).
Então aqui está o procedimento algorítmico:
Animação do algoritmo de Dijkstra, por Shiyu Ji da Wikipedia
- Algumas configurações: (1) bookkeep os vértices que visitamos: um conjunto (), (2) lembre-se das distâncias mais curtas conhecidas para cada vértice que usam apenas vértices descobertos: outro conjunto . A distância de cada vértice é inicialmente infinita, exceto pelo vértice de origem é 0.
visiteddistance(u) - Agora começamos a explorar: primeiro visitamos o vértice que tem o caminho mais curto conhecido até agora, digamos que é. (Inicialmente seria o vértice de origem).
u - Quando estamos no vértice, olhamos ao redor das bordas de saída. Cada aresta, digamos, nos dá um caminho para o vértice que usa o vértice como o último, mas apenas um passo. Se qualquer um deles for de fato um caminho mais curto para , ou o primeiro caminho que encontramos para , podemos atualizar nosso conjunto de caminhos mais curtos agora. Caso contrário, ignore e continue.
u(u,v)vuvv - Acabamos com o vértice, então o adicionamos ao nosso conjunto.
uvisited - Volte para o passo 2, continue explorando até que tenhamos visitado todos os vértices.
distance agora pode nos dizer as distâncias mais curtas globais, porque é usado para manter as distâncias mais curtas usando apenas nós visitados. E todos os vértices são visitados quando o algoritmo termina.
Acabamos de reinventar o algoritmo de Dijkstra. Claro, existem muitos outros algoritmos para encontrar o caminho mais curto. Mas a questão é que precisamos de um procedimento algorítmico para resolver o problema.
2. Validar princípios gerais por dedução
Como garantir que os princípios do algoritmo estejam corretos? Podemos aumentar nossa confiança testando o princípio contra mais exemplos de entrada, ou, mais eficazmente, podemos encontrar uma prova matemática rigorosa.
Como uma proposição a priori na filosofia, a correção de um algoritmo independe de sua execução. Em outras palavras, os testes não podem garantir a correção dos algoritmos. Precisamos provar isso.
Aqui está o fluxo básico da prova:
1. Para todos os vértices visitados, encontramos os caminhos mais curtos.
2. O destino é visitado.
3. Portanto, encontramos o caminho mais curto para o destino.
Não parecem um tanto familiares? Assim:
1. Todos os homens são mortais.
2. Sócrates é um homem.
3. Portanto, Sócrates é mortal.
Na verdade, esse é o silogismo, uma forma clássica de raciocínio dedutivo. Isso é praticamente o que os lógicos estão fazendo.
Outro fato histórico interessante: o conceito formal de computação foi criado pelos lógicos na década de 1930. Eles precisavam saber se certos problemas lógicos são realmente solucionáveis (para que pudessem evitar perder seu tempo resolvendo algo insolúvel). Para responder a isso, eles vêm com a noção de computabilidade.
Mais tarde, em 1936, Alonzo Church e Alan Turing desenvolveram a definição formal de Computabilidade, independentemente, ao mesmo tempo. Este artigo faz uma revisão histórica da computação.
O acerto da conclusão depende das duas primeiras premissas. Em nossa prova, a segunda premissa é trivial, já que nosso algoritmo está literalmente visitando todos os nós. No entanto, provar a primeira premissa, de que encontramos o caminho mais curto no momento em que visitamos um nó, precisa de algum trabalho.
A indução matemática pode ajudar. Na verdade, é uma das técnicas mais úteis para provar a correção de muitos outros algoritmos.
O fluxo geral é o seguinte. Primeiro, se um algoritmo funciona na entrada , e segundo, se o fato de que ele funciona na entrada implica que ele funciona na entrada também, então ele funciona para todas as entradas maiores ou iguais a . Neste ponto, você é capaz de garantir a correção do seu algoritmo.0nn+1 0
Para simplificar, vou encaminhá-lo para esta nota de aula para a prova completa deste algoritmo de localização de caminho.
Note que não devemos confundir indução matemática e indução filosófica. Pela definição filosófica, a indução matemática é um processo de raciocínio dedutivo, porque sua correção está contida em si mesma, sem quaisquer observações externas.
A lição é: quando criamos um algoritmo, ele deve ser capaz de lidar com todos os casos de execução possíveis.
Na prática, passar pela rigorosa prova matemática pode não ser a estratégia mais eficiente. Mas pelo menos queremos considerar o maior número possível de casos de execução, especialmente os contraditórios. Essa prática melhoraria a robustez do nosso código.
Você deve ter notado que, em nosso exemplo de algoritmo de localização de caminho, ele não funciona se o peso da borda for negativo. Você pode encontrar o motivo nesta nota de aula. Para manipular um gráfico de peso negativo, você pode usar o algoritmo de Bellman-Ford.
3. O problema da ontologia: estrutura de dados
Até agora nos convencemos de que temos um algoritmo correto. Mas isso é apenas metade da batalha.
A próxima pergunta é: como alimentar as informações nos computadores? Os seres humanos gostam de informações visualizadas, como gráficos ou histogramas. Mas os computadores de hoje só lidam com bits binários.
Precisamos criar uma estrutura de dados que contenha as informações essenciais. E deve ser eficiente para um programa processar ao mesmo tempo.
Vamos continuar nosso caminho encontrando exemplos. Um caminho é uma lista ordenada. Mas é irritante de lidar, em comparação com um inteiro. Note que em nosso algoritmo temos que encontrar o caminho mais curto a partir de nosso conjunto de caminhos descobertos. E depois iterar até o fim. Parece que temos que dedicar uma matriz ou memória para armazenar cada caminho.
Poderíamos fazer melhor? Observe que, em um caminho válido, aparições consecutivas de elementos devem corresponder a uma aresta no gráfico. Mas, já temos as informações de borda e elas são as mesmas para todos os caminhos. Por que não podemos nos livrar dessas informações redundantes?
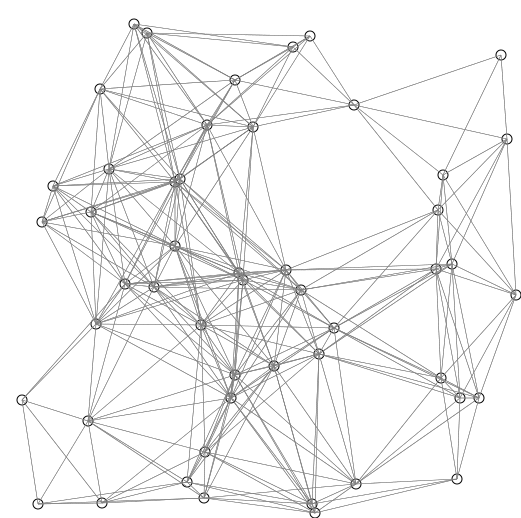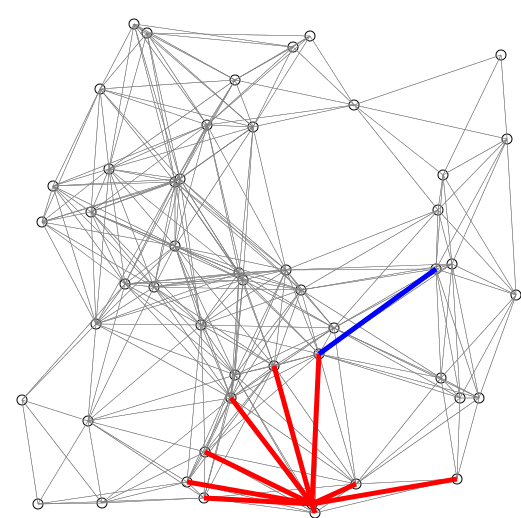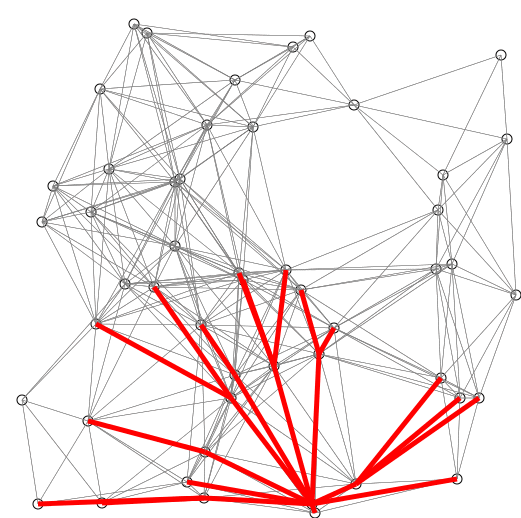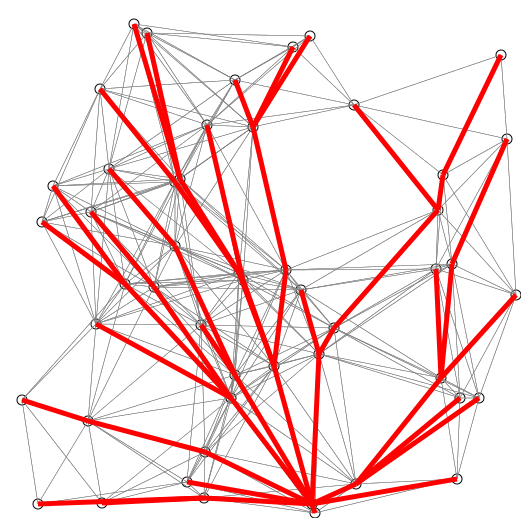
Bem, podemos nos livrar da lista. Acontece que, para reunir o caminho mais curto, o passo intermediário é determinar qual é o próximo salto que você precisa ir. Tudo o que precisamos para recuperar o caminho mais curto da origem A para qualquer nó de destino é apenas o gráfico em si, e a distância mais curta de A para cada nó.
Informações para recuperar o caminho mais curto de A para qualquer nó. (Números dentro de vértices denotam a distância de A.)
Uma representação visual está na imagem acima. Essa representação é eficiente em termos de memória. Também é mais eficiente para o programa processar.
É assim que ele constrói o caminho mais curto usando apenas o vetor de distância. Comece a partir do vértice de destino e um caminho vazio. Procure vértices intermediários através das bordas de entrada. Escolha aquele com o menor valor em . Adicione-o à cabeça do caminho. Repita até chegar à fonte. Esse truque, na verdade, tem uma notação formal, chamada back-tracking.distance
Os filósofos buscam a verdade eterna. E os programadores querem descobrir a estrutura de dados precisa que melhor captura a dinâmica das informações. Como você vê no exemplo de localização de caminho, tudo o que ele precisa para dar um caminho mais curto é apenas um vetor, dizendo as distâncias mais curtas para cada vértice. Isso vale para qualquer grafo, independentemente do número de vértices ou arestas.
4. Proposição a posteriori: depuração
A maioria dos programadores já passou por esse raciocínio toneladas de vezes. Aposto que esta é uma das partes mais difíceis e demoradas de qualquer tarefa de programação.
Por exemplo, falhas de segmentação em programas C geralmente são causadas por referências de ponteiro nulo. Aprendi isso depois de lidar com toneladas de falhas de segmentação C/C++. É claro que há casos mais sutis que se relacionam com hábitos pessoais de programação.
O exemplo a seguir é um erro de sintaxe cometido por um programador. A condição if deveria ter sido , mas o programador confundiu o operador lógico igual como um operador de avaliação. Isso ainda passará pela verificação do compilador, porque qualquer uma delas é a sintaxe correta.is_float==1 == =
if (is_float = 1) { // do something}
Trata-se de um processo de raciocínio indutivo. Seu diagnóstico de depuração só faz sentido se você tiver observado execuções de programa suficientes.
É aqui que entra o valor da prática. Não importa que tipo de técnicas você está aprendendo, você tem que reunir dados práticos suficientes. Caso contrário, você não teria experiência suficiente para conduzir a indução.
Você deve ficar de olho nos padrões recorrentes em seus códigos de bugs. Quando você encontra um bug, corrigi-lo não é suficiente. Você precisa de uma análise extra de causa-efeito em sua própria prática de programação. Pergunte-se: essa parte dos meus hábitos de programação é particularmente vulnerável a esse tipo de bug?
Então, por que isso importa?
Programar não é apenas escrever código, é uma forma sistemática de raciocinar. Porque o código, ou instruções, é apenas um meio para um fim. Com o desenvolvimento da técnica de síntese do programa, você pode nem se preocupar em escrever código e se depurar. Tudo o que importa é se você pode dizer ao computador o que fazer.
Como o primeiro passo para melhorar suas habilidades de programação, este artigo revela o padrão de raciocínio subjacente que talvez nem reconheçamos quando estávamos programando. A maioria de nós depende do subconsciente e da reflexão automática para terminar a maioria de nossas tarefas diárias. Mas de onde vem a melhoria? Primeiro vem de perceber alguma falácia ou erros que cometemos em nosso processo de raciocínio.
Para conselhos práticos, recomendo este artigo sobre como pensar como um programador, e este livro sobre o mesmo tema, mas com mais detalhes.
Referências
- Computação, Questões Filosóficas sobre. Matias Scheutz.
- A Tese de Church-Turing.
- Pense como um programador: uma introdução à resolução criativa de problemas. V. Anton Spraul.
Aprenda a programar gratuitamente. O currículo de código aberto do freeCodeCamp ajudou mais de 40.000 pessoas a conseguir empregos como desenvolvedores. Começar